javascript算法的二进制搜索树

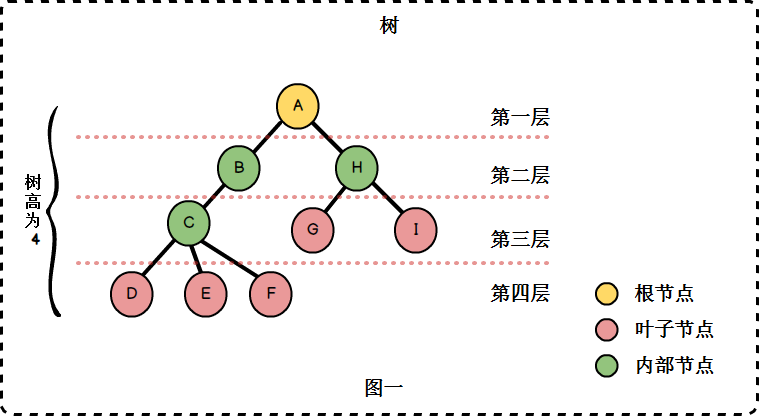
二叉树意味着该树的每个节点最多只能有两个子节点

二进制搜索树在二进制树的基础上还有一个附加条件，即，当二进制树插入一个值时，如果插入的值小于当前节点，则将其插入左节点，否则它被插入右节点；如果插入过程中，如果已经存在左节点或右节点，则继续根据上述规则进行比较，直到遇到新节点为止.

由于其唯一的数据结构，因此二叉搜索树的时间复杂度为O（h），无论是添加，删除还是搜索，其中h是二叉树的高度. 因此，二叉树应尽可能短，也就是说，左右节点应尽可能地平衡.

要构建二叉搜索树，请首先构建二叉树的节点类. 根据二叉树的特性，每个节点类都有一个左节点，一个右节点和值本身，因此该节点类如下:

class Node {
  constructor(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
}

接下来，构建一个二叉搜索树

class Tree{
  constructor(param = null) {
    if (param) {
      this.root = new Node(param);
    } else {
      this.root = null;
    }
  }
}

在这里this.root是当前对象的树.

由于二分搜索树的左侧子树小于节点，而右子树具有更大的节点，因此可以轻松地为二分搜索树编写新算法，如下所示:

insert(key) {
  if (this.root === null) {
    this.root = new Node(key);
  } else {
    this._insertNode(this.root, key);
  }
}
_insertNode(node, key) {
  if (key < node.key) {
    if (node.left === null) {
      node.left = new Node(key);{1}
    } else {
      this._insertNode(node.left, key);{2}
    }
  } else if (key > node.key) {
    if (node.right === null) {
      node.right = new Node(key);{3}
    } else {
      this._insertNode(node.right, key);{4}
    }
  }
}

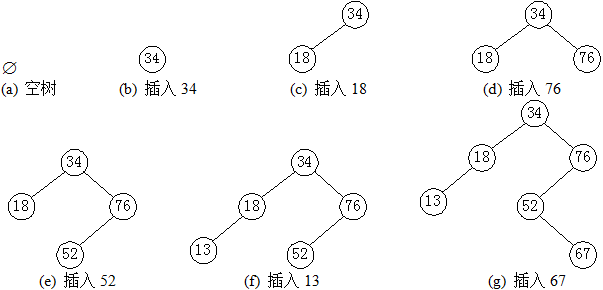
上面的代码首先确定新添加的密钥和当前节点的密钥的大小. 如果它很小，它将递归遍历左子节点，直到找到一个空的左子节点为止；否则，它将遍历左子节点. 如果它大于当前节点，则相同. 上面的代码{1} {2} {3} {4}可以更改this.root的值的原因是因为JavaScript函数是按值传递的，并且参数是非原始类型的，例如对象在这里，对象的值是内存，因此每次都会直接更改this.root的内容.

二叉搜索树分为三种遍历方法: 第一顺序，中间顺序和最后顺序.

inOrderTraverse(callback) {
  this._inOrderTraverse(this.root, callback);
}
_inOrderTraverse(node, callback) {
  if (node) {
    this._inOrderTraverse(node.left, callback);
    callback(node.key);
    this._inOrderTraverse(node.right, callback);
  }
}

如上所述，它是中间顺序遍历.

这里要了解的一件事是递归. 请注意，函数的执行可以抽象为数据结构-堆栈. 为了执行功能，维护堆栈以存储功能的执行. 每次函数递归时，它将当前执行环境放在堆栈上并记录执行位置. 以上面的代码为例，有以下数据

它将从11开始，对堆栈执行{1}，然后转到7，然后对堆栈执行{1}，然后到5，对堆栈执行{1}，然后到3，执行{1 }到堆栈上，此时，发现节点3的左子节点为空，因此堆栈开始弹出. 这时，弹出节点3的执行环境，执行{2}，{3}，还发现3的右子节点为空，{3}递归执行完成后，弹出向上执行节点5，执行{2} {3}，然后弹出7，执行{2} {3}到堆栈上，当执行{3}时，发现节点7具有正确的节点，因此继续执行{ 1}到节点8，然后执行{1}，8没有左子节点，执行{1}二叉排序树算法，执行{2} {3}，依此类推.

预定顺序和中间顺序之间的区别在于，它首先访问节点本身，即代码执行的顺序为2 1 3.

顺序相同，执行顺序为1 3 2

不难发现，无论中间顺序如何，左节点始终都是递归的. 遍历左侧节点时，将再次弹出堆栈，遍历这些节点. 它们和访问节点本身的时间之间的唯一区别.

搜索非常简单. 您可以基于左子节点小于该节点，右子节点大于该节点的原则做出循环判断.

search(value) {
  return this._search(value, this.root);
}
_search(value, node) {
  if (node === null) {
    return false;
  } else if (value > node.value) {
    return this._search(value, node.right);
  } else if (value < node.value) {
    return this._search(value, node.left);
  } else {
    return true;
  }
}

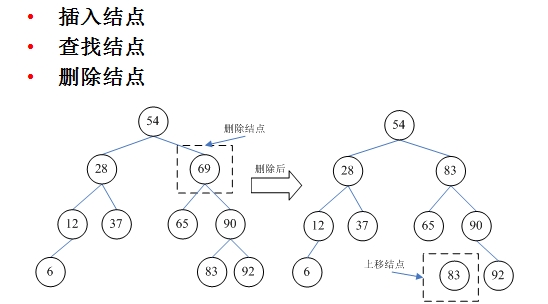
删除操作比较复杂，需要根据不同情况进行判断

首先确定节点是否具有左子树. 如果没有左子树，则直接用删除的节点替换右子树的根节点；

如果有，请用删除的节点替换右子树的最小节点；

remove(value) {
  this.root = this._removeNode(this.root, value);
}
_removeNode(node, value) {
  if (!node) {
    return null;
  }
  if (value > node.value) {
    node.right = this._removeNode(node.right, value);
    return node;
  } else if (value < node.value) {
    console.log(value);
    node.left = this._removeNode(node.left, value);
    return node;
  } else {
    // 如果左右子节点都没有
    if (!node.left && !node.right) {
      return null;
    }
    // 如果只有一个子节点
    if (node.left === null) {
      return node.right;
    }
    if (node.right === null) {
      return node.left;
    }
    // 如果同时拥有两个节点，就取有子节点最小值来替换当前被删除节点
    const minNode = this._minNode(node.right);
    node.value = minNode.value;
    node.right = this._removeNode(node.right, minNode.value);
    return node;
  }
}

通常，通过研究这个简单的二进制搜索树，我重新认识了递归. 以前对递归的理解只是一些简单的理论概念. 这种深入的实践使我再次了解了递归. 加深了很多.

这使我想起了数学的研究. 数学的理论公式易于记忆和掌握. 如果知识点的掌握程度很高二叉排序树算法，那么在您实际练习它之前，请先看看公式的掌握程度. 可以是2分，因为公式非常简单，只需几句话和几条原则，但是遇到的问题是千变万化的. 只有在将理论付诸实践后，经过各种实践的磨合和破坏，它才能真正理解其奥秘.

本文来自本站，转载请注明本文网址：
http://www.pc-fly.com/a/jisuanjixue/article-248651-1.html