搜索算法（1）: 二进制搜索树BST

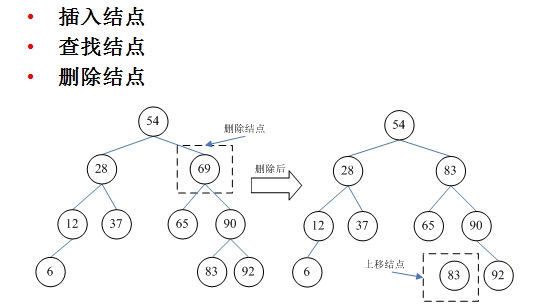
最近查看Java集合类时，有许多用于高效搜索的低级结构，例如哈希，红黑树等也被遗忘了二叉排序树查找算法，因此这只是对Java集合类的系统总结. 搜索相关的结构算法

查找表: 相同类型的数据元素的集合

搜索: 它分为静态搜索（正义搜索）和动态搜索（包括插入元素和删除元素）-静态搜索: 顺序搜索（遍历），半搜索，索引相对简单，主要分析和分析动态搜索权

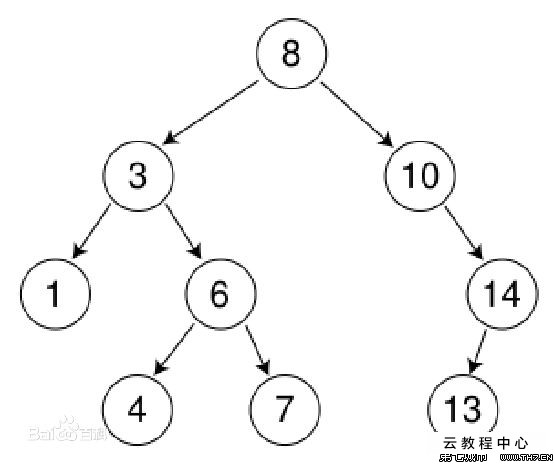
二进制搜索树（BST）是空树或满足以下要求的二进制树:

1. 如果左子树不为空，则左子树上任何节点的键值小于根节点的键值

2. 如果右子树不为空二叉排序树查找算法，则右子树上任何节点的键值都大于根节点的键值

3. 它的左和右子树分别是二叉搜索树

自然

实现Java基本操作

定义BST树结构如下:

public class BTreeNode {
        int val;//节点的关键字值
        BTreeNode left;//左子树
        BTreeNode right;//右子树
        BTreeNode(int x) { val = x; }
    }

搜索算法实现

//找到目标值返回该值对应的树节点，找不到返回null
    public BTreeNode searchBST(BTreeNode node,int des){
        if(node == null)
            return null;
        if(node.val == des)
            return node;
        if(des > node.val)
            return searchBST(node.right,des);
        else
            return searchBST(node.left,des);
    }

搜索时间复杂度分析: 复杂度与BST的树结构有很大关系. 如果所有节点均按关键字递增或递减的顺序构造，则构造的二叉树将退化为. 单链结构已变为线性复杂度O（n）. 最好的情况是节点尽可能靠近根节点，因此平均和最佳情况下的搜索时间为O（logn），即树的高度.

插入算法说明

//返回插入元素之后的新的树结构
    public BTreeNode insertBST(BTreeNode node,int des){
        if(node == null)//如果根节点为空，那么新建一个树返回
            return new BTreeNode(des);
        if(des == node.val)//如果跟根节点的键值等于插入值，那么查找成功，返回原先的树即可
            return node;
        if(des > node.val)//递归调用插入
            node.right = insertBST(node.right,des);
        else
            node.left = insertBST(node.left,des);
        return node;
    }

基本上基于搜索算法，您无需插入找到的元素，只需返回原始树即可；如果插入的值大于节点的键值，则问题将转换为插入到节点的右子树中. 其值是关键字的节点与小于该值的情况相似，请记住返回结束

删除算法说明

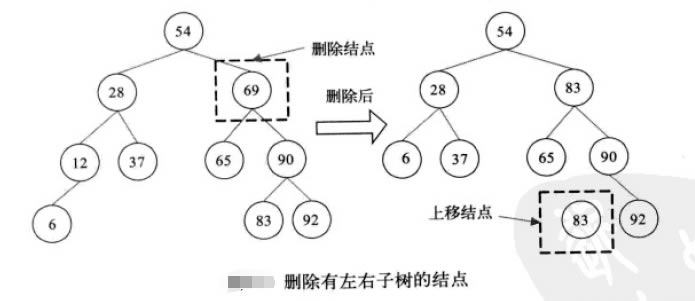
在BST中删除某个关键字的节点，以确保删除后整个树结构保持有序，有以下三种删除情况:

public BTreeNode removeBST(BTreeNode node,int des){
        if(node == null)
            return null;
        if(des == node.val){//查找成功，开始删除
            if(node.left == null && node.right == null)
                return null;//左右子树都是空的，直接返回null
            if(node.left == null && node.right != null)
                return node.right;//左子树为空的时候，右子树顶点就是新的头了
            if(node.left != null && node.right == null)
                return node.left;//右子树为空的时候，左子树顶点就是新的头了
            else{//两个子树都不为空
                BTreeNode tmp = node.left;
                while(tmp.right != null){
                    tmp = tmp.right;//找到左子树的最右结点
                }
                node.val = tmp.val;//直接替换值
                node.left = removeBST(node.left,tmp.val);//将左子树的最有结点删除
            }
        }
        else if(des > node.val)
            node.right =  removeBST(node.right,des);
        else
            node.left =  removeBST(node.left,des);
        return node;
    }

在实现过程中注意递归结束条件，以便当删除的元素不存在时，它将返回到原始树结构

本文来自本站，转载请注明本文网址：
http://www.pc-fly.com/a/jisuanjixue/article-251013-1.html