

|
几何画板是一个作图和实现动画的辅助教学软件,用户可以根据教学需要编制出相关的图像和动画过程。几何画板是适用于数学、平面几何、物理的矢量分析、作图,函数作图的动态几何工具。 在射影几何中有一个重要定理,就是帕斯卡定理,它的定义是如果一个六边形内接于一条二次曲线(圆、椭圆、双曲线、抛物线),那么它的三对对边的交点在同一条直线上。 由于六边形的存在多种情况,帕斯卡定理的图形也存在多种,它们虽然看起来截然不同,但均为帕斯卡定理,证明它们的方法也是相同的。 比如:已知圆内接六边形 ABCDEF 的边 AB、DE 延长线交于点 G,边 BC、EF 延长线交于点 H,边 CD、FA 延长线交于点 K,则 H、G、K 三点共线,下面就以此题来进行证明。 用几何画板验证帕斯卡定理的步骤如下: 步骤一 画圆内接六边形 ABCDEF打开课件制作工具,选择圆工具任意画一个圆,然后使用点工具在圆上画出点A、B、C、D、E、F,接着用线段工具依次连接相连两点,这样就画出了圆的内接六边形。 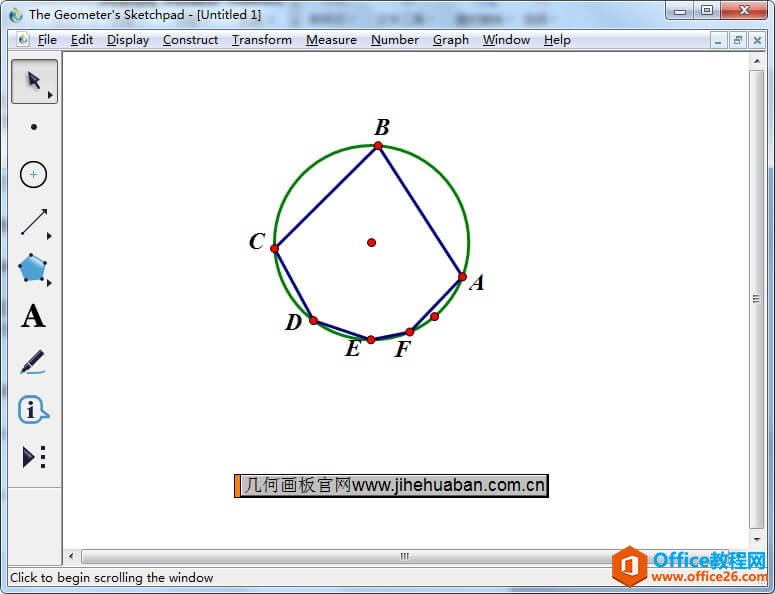 图1:快速画圆内接六边形 步骤二 验证三对对边的交点在同一条直线上1.延长边 AB、DE 交于点 G 选择射线工具,作射线BA、DE,两条射线相交,交点标记为点 G,如下图所示。 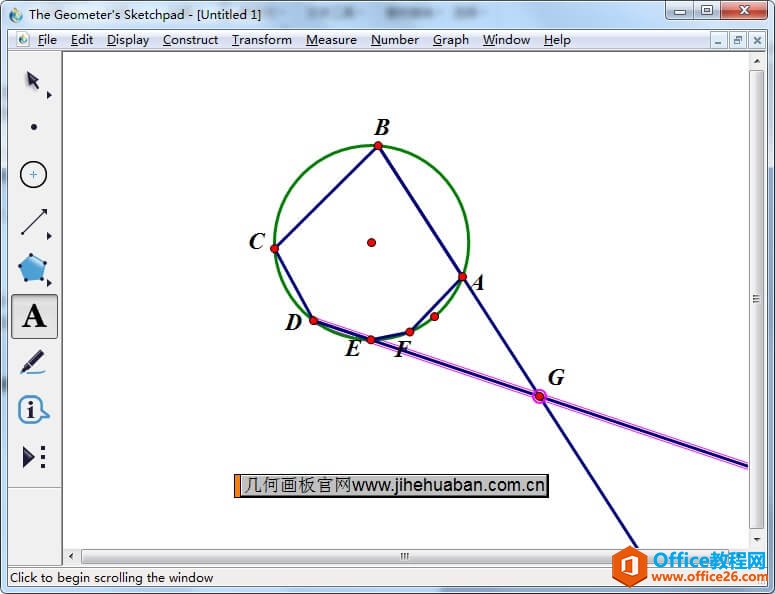 图2:作射线BA、DE交于点G 2.延长边 BC、EF 交于点 H 选择射线工具,作射线BC、EF,两条射线相交,交点标记为点 H,如下图所示。 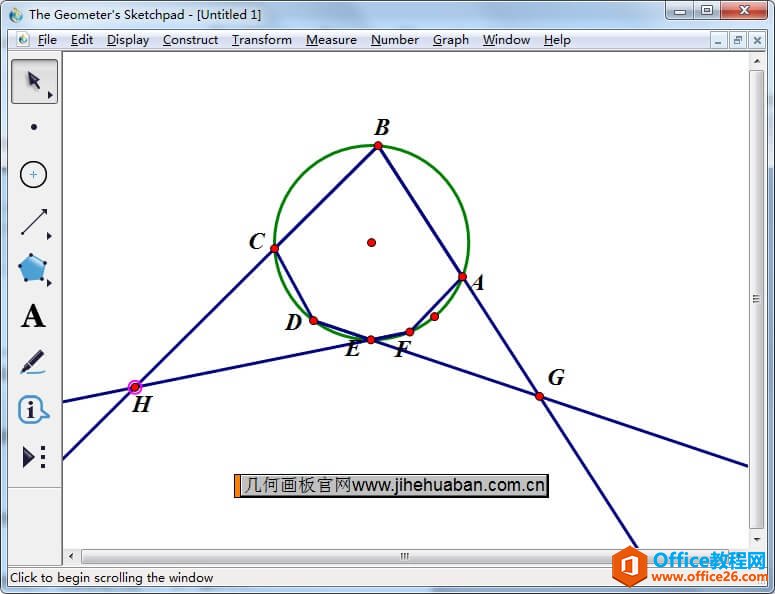 图3:延长射线BC、EF交于点H 3.延长边CD、FA 交于点 K 选择射线工具,作射线CD、FA,两条射线相交,交点标记为点 K,如下图所示。 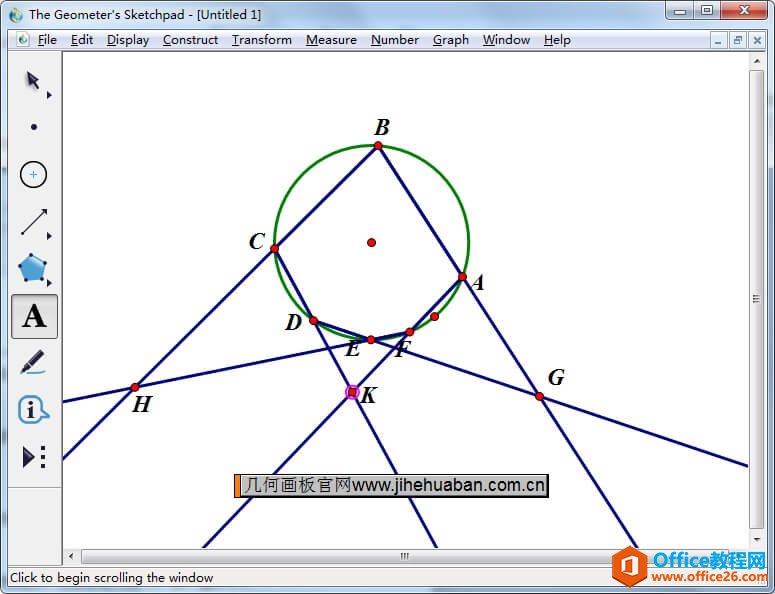 图4:延长射线CD、FA交于点K 4.连接点G、H、K,验证三个交点共线 选择直线工具,作直线HG,发现点G、H、K三点在同一条直线上,从而就验证了帕斯卡定理。 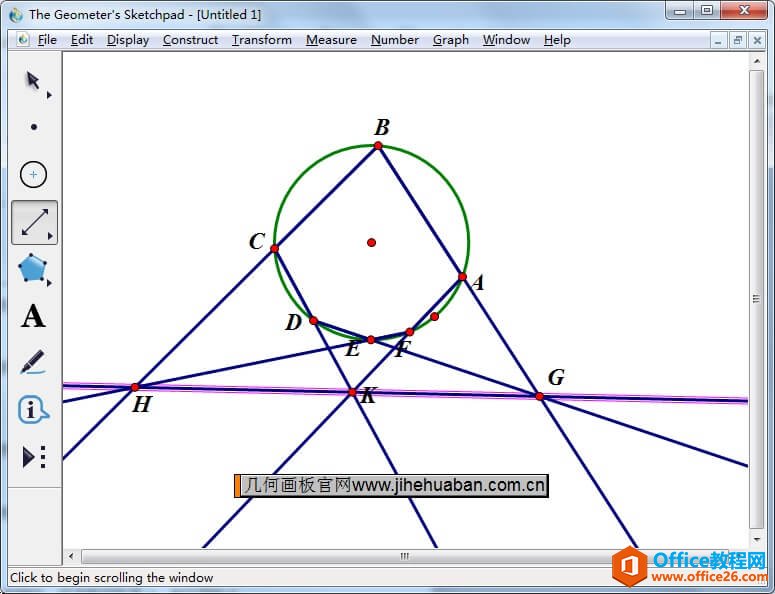 图5:作直线HG验证三点共线 几何画板提供丰富而方便的创造功能使用户可以编写出自己需要的教学课件。 |
温馨提示:喜欢本站的话,请收藏一下本站!