几何画板如何制作贝塞尔曲线

贝塞尔（Bezier）曲线又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋。贝塞尔曲线是计算机图形学中相当重要的参数曲线，利用几何画板这一强大的几何绘图工具，也可以轻松绘制出贝塞尔曲线，下面将详细介绍利用几何画板绘制贝塞尔曲线的方法。

绘制贝塞尔曲线的具体操作步骤如下：

步骤一 建立直角坐标系。打开几何画板，单击“绘图”菜单，选择“定义坐标系”命令建立直角坐标系。

步骤二 在平面内任意画出4点A、B、C、D，并度量出它们的横纵坐标x_A，y_A，x_B，y_B，x_C，y_C，x_D，y_D。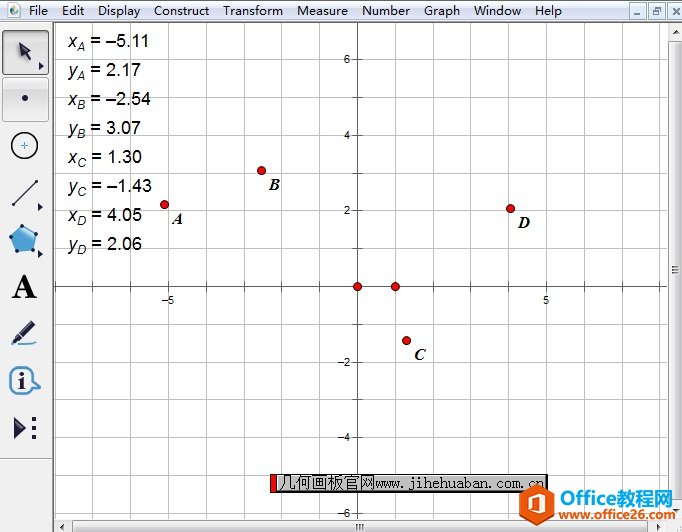

步骤三 创建2个函数。单击“数据”——“新建函数”命令，创建以下函数：

f(x)=x_A*(1-x)³+3*x_B*x*(1-x)²+3*x_C*x²*(1-x)+x_D*x³

g(x)=y_A*(1-x)³+3*y_B*x*(1-x)²+3*y_C*x²*(1-x)+y_D*x³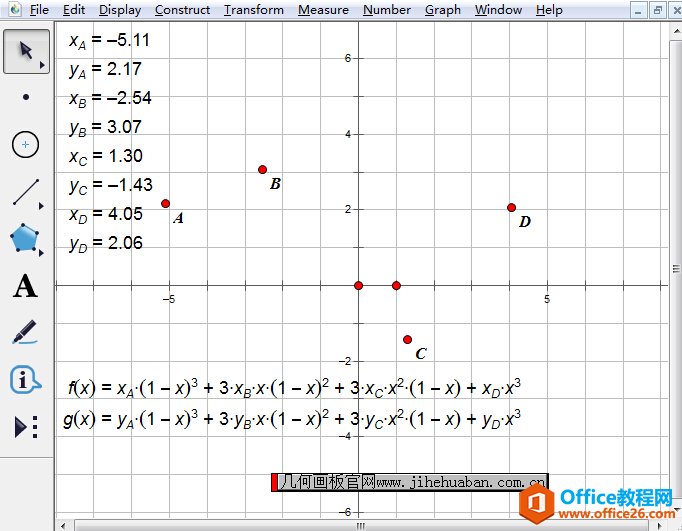

步骤四 选中f(x)、g(x)，单击“绘图”菜单，选择“绘制参数曲线”命令，在弹出的绘制参数曲线对话框点击“绘制”按钮，这样一条Bezier曲线就产生了。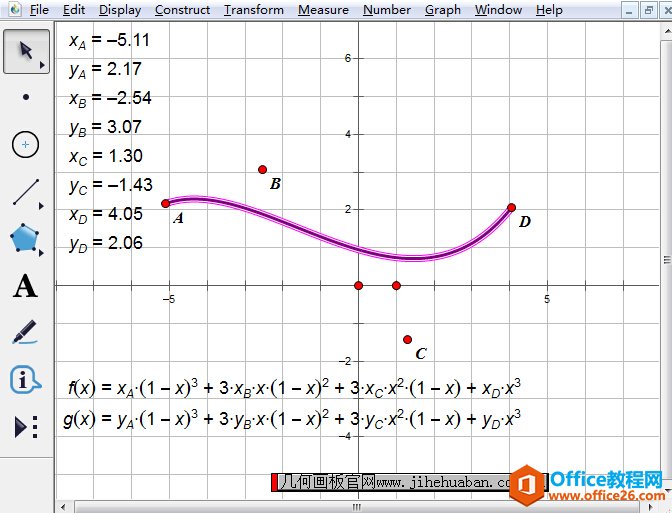

以上给大家介绍了利用几何画板绘制贝塞尔曲线的方法，主要运用了几何画板参数曲线功能。贝塞尔曲线就是这样的一条曲线，它是依据四个位置任意的点坐标绘制出的一条光滑曲线。