几何画板 如何根据绘制导函数图像求函数极值

数学中函数的极值不仅在实际问题中占有重要的地位，而且也是函数性态的一个重要特征，下面将通过举例介绍几何画板函数极值和单调区间的求解方法。

具体的操作步骤如下：

1.打开几何画板软件，“绘图”——“绘制新函数”，在函数编辑器中输入下图中的函数解析式，点击“确定”即可。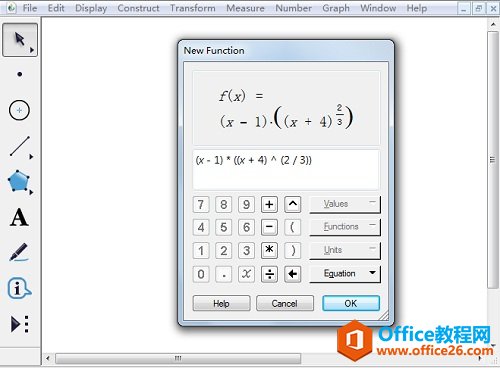

2.右键函数解析式，选择“定义导函数”，出现导函数解析式。右键导函数，选择“绘制函数”，在绘图区域中会出现原函数的导函数（蓝色）。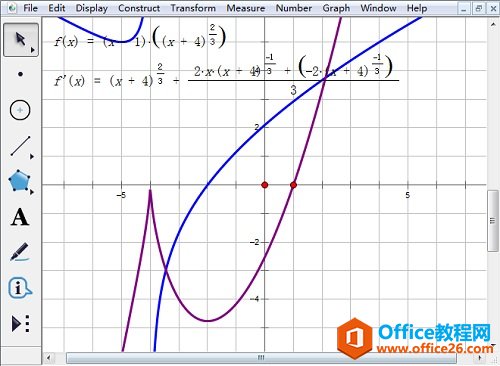

3.选定绘制的导函数图像和x轴，“构造”——“交点”，得到点A。因为原函数在点B处不可导，“绘图”——“绘制点”，绘制点B（-4，0）。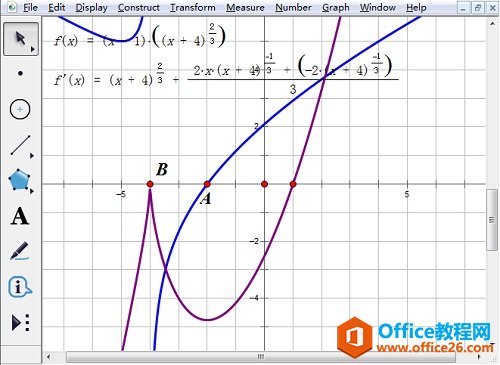

4.选定点B和点A，“度量”——“横坐标”，横坐标值就是原函数单调区间的转折点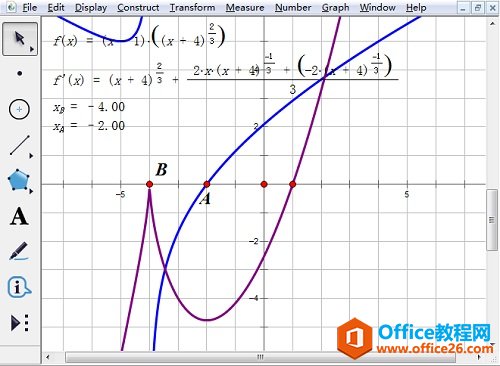横坐标。

说明：在绘制点B处，导数不存在，故原函数在点B处有极大值0，在点A处有极小值。

以上向大家介绍了几何画板函数极值的求解方法，主要运用了几何画板定义导函数功能，大家多练习几次，就可以熟练掌握了。