

|
几何画板是一个作图和实现动画的辅助教学软件,用户可以根据教学需要编制出相关的图像和动画过程。几何画板是适用于数学、平面几何、物理的矢量分析、作图,函数作图的动态几何工具。 谢尔宾斯基地毯和谢尔宾斯基三角形基本是同一种构造,只是由三角形变成了正方形,难度因此增大。下面将详细介绍用几何画板画谢尔宾斯基地毯的方法。 分析:取正方形将其9等分,得到9个小正方形,舍去中央的小正方形,保留周围8个小正方形。然后对每个小正方形再9等分,并同样舍去中央正方形。按此规则不断细分与舍去,直至无穷。谢尔宾斯基地毯的极限图形面积趋于零,小正方形个数与其边的线段数目趋于无穷多,它是一个线集,图形具有严格的自相似性。 具体的绘图步骤如下: 1.打开几何画板软件,在平面上任意画线段AB,以线段AB为边长构造正方形ABCD。 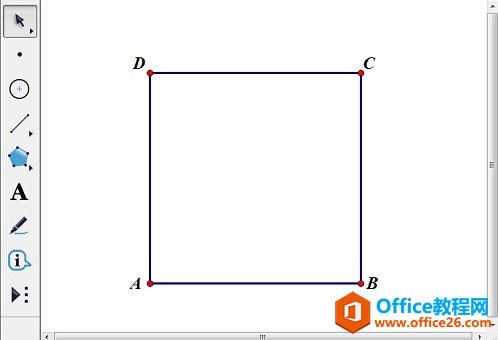 ? ?以线段AB为边长构造正方形ABCD 2.以点A为缩放中心,将点B、D缩放为1/3得到E、F;以D为缩放中心,将点A、C缩放为1/3得到G、H。同理得到点I、J、K、L。连接各点,将正方形九等分。 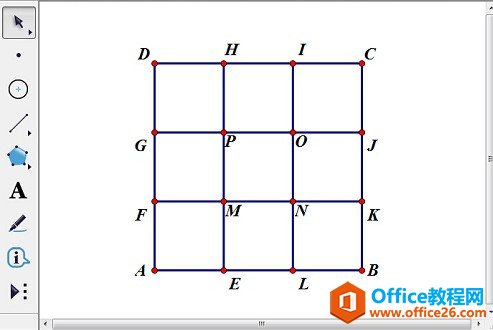 ? ?通过缩放各点将正方形ABCD九等分 3.点击“数据——新建参数”新建参数n,数值改为2。依次点击A、B两点(注意:这两点是你最开始画出的线段的两个端点)和参数n,按住shift键,点击“变换——深度迭代”打开迭代对话框,选择G、P两点,点击“结构”——“添加新的映射”,选择P、O两点,继续添加新的映射,选择O、J;F、M;N、K;A、E;E、L;L、B。(注意:中间的M、N两点不要点)点击“迭代”,完成迭代制作。 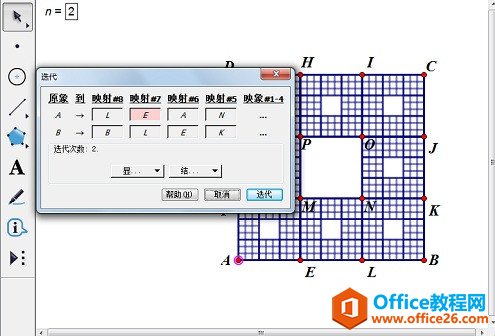 ? ?对正方形的等分点执行深度迭代 4.填充中间的正方形MNOP,度量MNOP的面积,选择该度量结果和填充的正方形,单击“显示”——“颜色”——“参数”,在弹出的对话框单击“确定”。 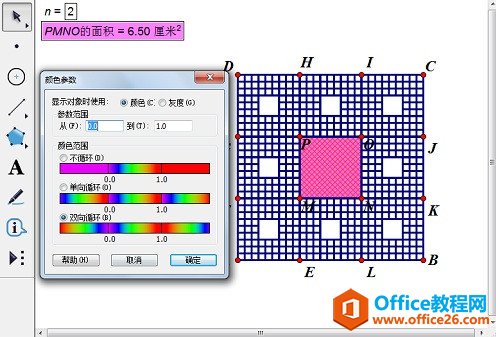 ? ?填充正方形MNOP并设置颜色参数 5.最后,选中所有点,按Ctrl+H,隐藏不必要的点。 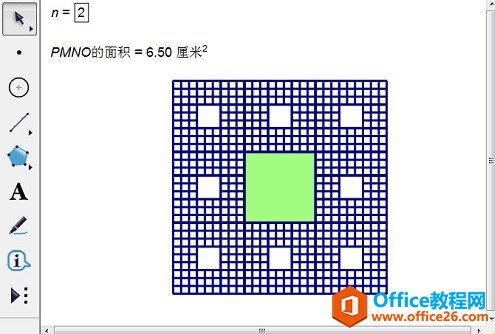 ? ?隐藏所有点完成谢尔宾斯基地毯制作 温馨提示:改变正方形ABCD的大小,则正方形MNOP的颜色随它的面积变化而变化。通过改变参数n的数值来观察谢尔宾斯基地毯的不同。 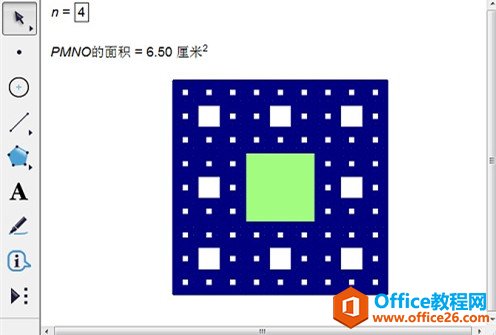 ? ?改变参数n来观察谢尔宾斯基地毯的不同 以上向大家介绍了几何画板画谢尔宾斯基地毯的方法,主要是运用了几何画板深度迭代功能。学了这个教程,大家肯定会有这样的疑问:谢尔宾斯基三角形是怎么画的呢? 几何画板提供丰富而方便的创造功能使用户可以编写出自己需要的教学课件。 |
温馨提示:喜欢本站的话,请收藏一下本站!